
1. 합병 정렬
1-1. 합병 정렬? 병합 정렬?
1-2. 합병 정렬이란?
1-3. 움짤로 보는 예시
1-4. 글로 보는 예시
1-5. 소스코드
1-6. 합병 정렬의 시간 복잡도
1-7. 합병 정렬은 얼마나 빠를까?
1. 합병 정렬
1-1. 합병 정렬? 병합 정렬?
처음에 이름이 굉장히 헷갈렸다. (합병이 병합이고 병합이 합병 아닌가...? 🥴)
결론부터 말하자면 둘 다 맞는 말이다. 둘 다 사용해도 된다.
개인적으로 궁금해서 둘의 그 미묘한 차이를 알고 싶어 알아봤는데
- 합병: A와 B가 합쳐져 C가 만들어짐
- 병합: A가 B의 일부가 되거나 B가 A의 일부가 됨
이 블로거에 의하면 위와 같은 차이가 있다고 한다.
만약 이게 사실이라면 음,,, 나는 합병 정렬이 오늘 배울 내용과 더 적합하지 않을까..?라고 생각한다.
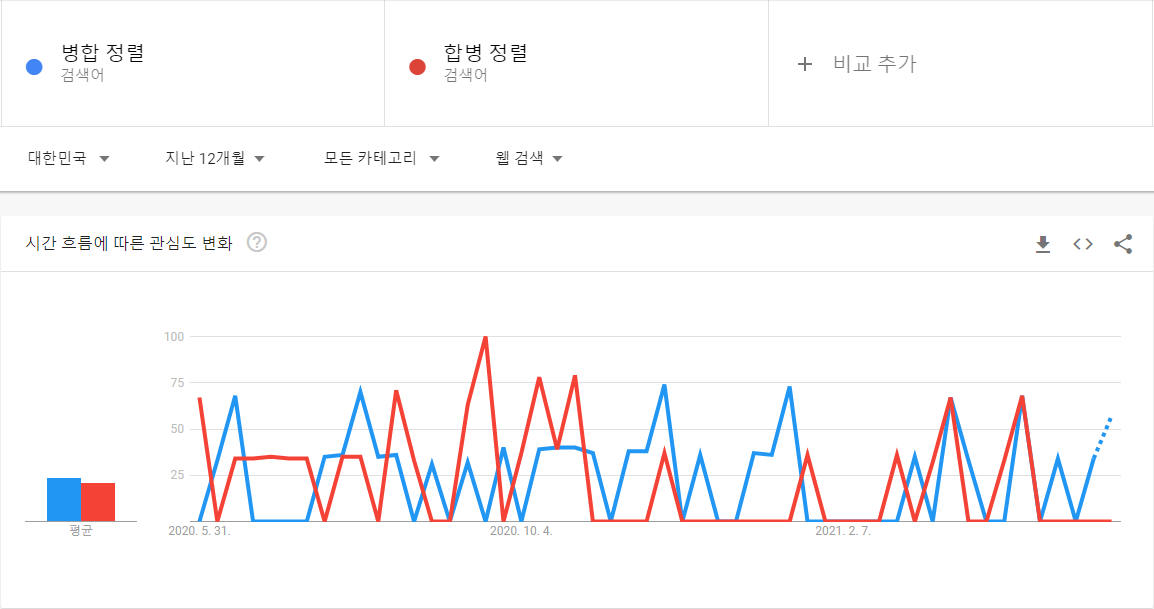
사람들이 둘 중 어떤 걸로 검색을 많이 할까 알아보니 병합이 아쭈 쪼꼼 많았다. (쳇)
1-2. 합병 정렬이란?
퀵 정렬과 마찬가지로 분할 정복 알고리즘을 사용한 정렬 방법이다.
분할을 이용하면 정렬 속도가 빨라지는 이유는 퀵 정렬 포스팅의 [목차 1-4]에서 잠시 언급했었다.
퀵 정렬은 평균적인 속도가 매우 빠른 대신 최악의 경우는 O(n²)의 시간 복잡도를 가진다는 단점이 있었다.
빠를 때는 엄청 빠른데 느릴 때는 엄청 느리다는 것이다.
즉, high risk high return!
하지만 합병 정렬은 최악의 경우에도 O(nlogn)의 시간 복잡도를 보장한다는 장점이 있다.
반면 추가적인 저장 공간을 필요로 한다는 단점이 있으니 상황에 맞는 정렬 방법을 택하면 된다.
그래서 합병 정렬은 어떤 메커니즘으로 돌아가는 걸까?
다음 목차에서 알아보자.
1-3. 움짤로 보는 예시

합병 정렬은 배열을 반으로 쪼개고 쪼개고.... 1개가 될 때까지 계속 쪼갠다음
다시 합병 & 정렬을 하며 배열을 완성시키는 방법이다.
대충 느낌만 쓰윽 보고 다음 목차에서 더 자세히 알아보자.
1-4. 글로 보는 예시

합병 정렬의 전체적인 개념은 그렇게 어렵지 않다.
위 그림만 봐도 대충 어떻게 진행되는지 감이 올 것이다.
절반으로 뚝 뚝 분할하다가 각각의 원소가 1개가 되면
대소 비교를 통해 정렬하면서 합병을 하면 된다.
다만 이걸 코드로 구현해내기가 쪼오끔 까다롭긴 한데 천천히 알아보도록 하자.
- 분할

우선 8개의 숫자를 분할한다고 생각해보자.
(첫 번째 인덱스 + 마지막 인덱스) / 2를 하면 중간 인덱스를 구할 수 있다.
즉, start ~ mid 이렇게 한 그룹을 이루게 되고
mid+1 ~ end 이렇게 한 그룹을 이루게 된다.

이렇게 위 그림처럼 분할할 수 있을 것이다.
이전 배열의 mid 인덱스가 왼쪽 파티션에서는 end가 되고
mid 인덱스에 +1 한 값이 오른쪽 파티션에서는 start가 된다는 점을 염두에 두고
원소가 1개가 될 때까지 계속 분할해나가면 된다.
물론 원소가 1개인지 아닌지 검사하는 식도 넣어주어야 한다.
start < end 인지 검사해주면 된다.
- 합병

연습 삼아 5, 6 그리고 2, 8을 합병해보자.
우선 5 > 2 이니까 2를 먼저 넣어준다.

그다음 5 < 8 이니까 5를 넣어준다.

그다음 6 < 8 이니까 6을 넣어준다.

남은 값을 마저 넣어주면 합병이 완료된다.
이런 식으로 계속 합병을 해나가면 합병 정렬이 완료된다.
1-5. 소스코드
public class Test {
public static int[] tmp; // 배열의 값을 잠시 복사해둘 공간
public static void main(String[] args) throws IOException {
int[] arr = { 3, 1, 7, 4, 5, 6, 8, 2 };
mergeSort(arr);
}
public static void mergeSort(int[] arr) {
tmp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1);
}
private static void mergeSort(int[] arr, int start, int end) {
// 원소가 2개 이상이라면
if(start < end) {
// 중앙 값을 구하고
int mid = (start + end) / 2;
// 중앙을 기준으로 2개의 그룹으로 분할
mergeSort(arr, start, mid);
mergeSort(arr, mid+1, end);
// 정렬 후 병합
merge(arr, start, mid, end);
}
}
private static void merge(int[] arr, int start, int mid, int end) {
// 배열 복사
tmp = arr.clone();
/*
* part1: 왼쪽 그룹의 시작 인덱스
* part2: 오른쪽 그룹의 시작 인덱스
* index: 정렬된 값을 병합된 배열의 어떤 위치에 넣어야하는 지
*/
int part1 = start;
int part2 = mid + 1;
int index = start;
// 두 그룹중 한쪽의 원소가 오링날때까지 반복 (정렬 & 합병)
while(part1 <= mid && part2 <= end) {
if(tmp[part1] <= tmp[part2]) {
arr[index++] = tmp[part1++];
} else {
arr[index++] = tmp[part2++];
}
}
// 왼쪽 그룹의 원소가 남는 경우 처리
// (오른쪽 그룹의 원소가 남는 경우는 따로 처리하지 않아도 된다)
for(int i=0; i<=mid-part1; i++) {
arr[index+i] = tmp[part1+i];
}
}
}소스코드는 위와 같다.
설명을 주석으로 자세히 달아두었지만 약간의 설명이 필요할 듯하다.
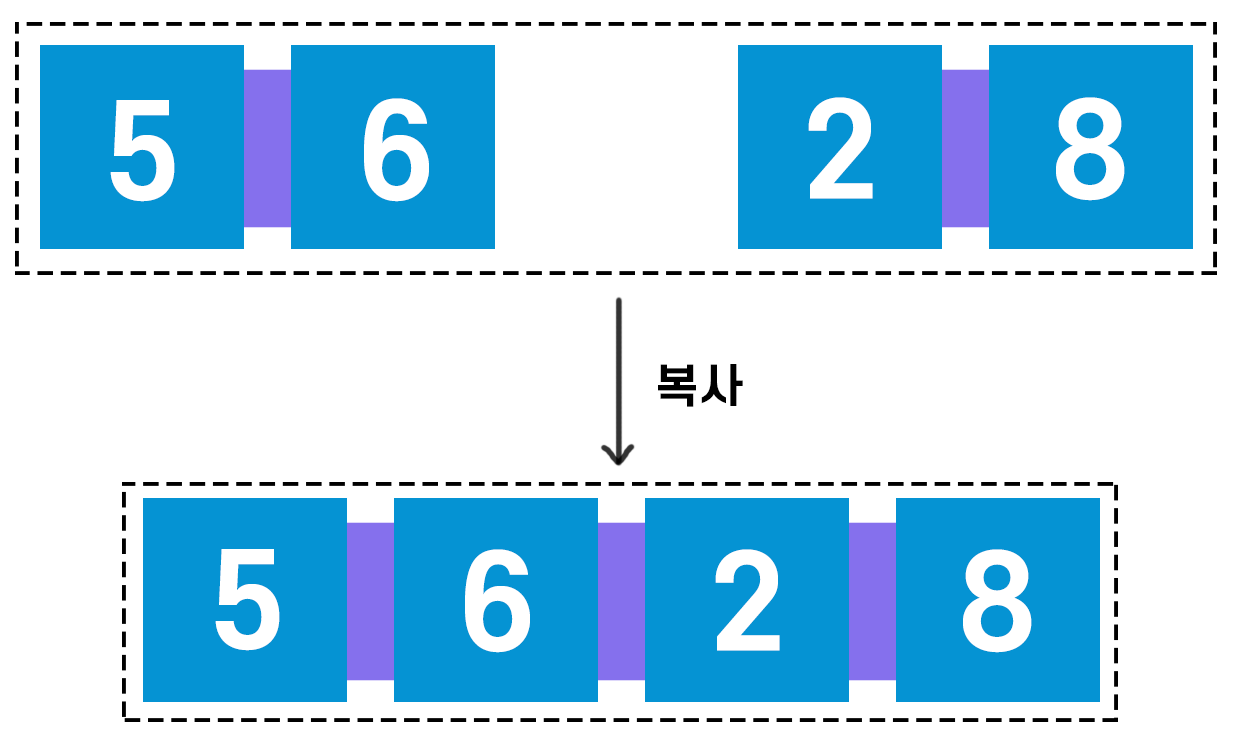
우선 배열을 복사하는 이유에 대해 설명이 필요하다.
[목차 1-4]에서는 이해를 돕기 위해 합병을 할 때 마치 빈 배열을 이용하는 것처럼 보여주었지만
실제로는 복사된 배열에다가 값을 집어넣는다.
그 이유에 대해서 설명을 하려고 한다.

합병을 할 때 대소 비교를 하며 값을 정렬하게 되는데
이때 왼쪽 파티션이든 오른쪽 파티션이든 어느 한쪽에는 값이 무조건 남게 되어있다.
위 그림을 보면 '6'과 '8'을 비교해서 작은 값인 '6'을 넣고 나면
'8'은 더 이상 비교할 대상이 없어진다.
이런 경우 남아있는 값을 이어서 넣어주는 작업을 따로 해야 하는데
이 과정을 생략하기 위해 복사된 배열을 사용한다는 것이다.
애초에 4개짜리 배열이 빈 배열이 아니라 복사된 배열이었다면
5, 6, 2, 8이 들어있었을 테고 그렇다면 마지막으로 남은 '8'을 넣어주는 작업이 필요 없기 때문이다.
하지만 이 방법은 마지막으로 남은 값이 오른쪽 파티션에 있어야 한다.
즉, 왼쪽 파티션에 값이 남아있는 경우를 처리해주는 로직이 추가로 필요하고
그 로직이 merge 메서드 안에 있는 맨 마지막 for문 부분이다.
만약 설명이 이해가 잘 안 간다면 이 영상의 5분 59초 부분을 보고 오자.
1-6. 합병 정렬의 시간 복잡도

합병 정렬의 시간 복잡도는 n개의 데이터를 가지고 logn단계를 거치기 때문에 O(nlogn)이 된다.
퀵 정렬은 비대칭으로 분할이 될 수 있기 때문에 O(n²)인 반면에
합병 정렬은 언제나 절반씩 분할이 되기 때문에 언제나 항상 O(nlogn)의 시간 복잡도를 가진다.
1-7. 합병 정렬은 얼마나 빠를까?
이번에도 역시 실제로 정렬 속도가 얼마나 되는지 궁금해서 테스트를 해보았다.
그런데....

.
.
.
.
.
.
.

아니 이게 어떻게 된 일이여...
분명 내 예상대로라면 합병 정렬은 퀵 정렬하고 속도가 비슷해야 하는데 어마어마한 차이가 났다.
다른 블로거들이 올려놓은 속도 비교 결과에서도 적게는 1.x배에서 많게는 5.x배 정도까지 차이가 났는데 이건 뭐...
그래서 이렇게 많이 차이 나는 이유에 대해 나름 조사해봤다.
- 첫 번째 이유
// 메서드를 이용한 복사
tmp = arr.clone();
// for문을 돌며 복사
for(int i=0; i<arr.length; i++) {
tmp[i] = arr[i];
}소스 코드에서 배열을 복사하는 메서드를 사용했었는데
메서드를 사용하는 것이 for문을 직접 돌며 복사하는 것보다 1.5~2배 정도 느렸다.
나는 이클립스에서 제공하는 메서드가 당연히 뭔가 최적화되어있고 빠를 거라 생각했는데... 그렇지만도 않은 듯하다.
그래서 우선 이게 첫 번째 원인이었다.
- 두 번째 이유
두 번째 이유에서 바로 합병 정렬의 단점이 나온다.
추가적인 공간을 차지한다는 것뿐만 아니라 배열을 복사하는 시간이 오래 걸린다는 것이다.
그래서 데이터의 개수를 100,000개에서 2000개로 줄여 복사하는 작업을 줄여보았다.

결과는 위와 같았다. 이번에는 합병 정렬이 오히려 버블 정렬보다도 느린 속도를 보여주었다.
그래서 나는 이 이유에 대해 다음과 같이 추측해보았다.
다른 블로그에 올라온 정렬 시간 비교글들은 대부분 C언어로 테스트한 것이었다.
그리고 Java로 테스트한 다른 블로그 글과 내 결과를 비교해보니 거의 흡사했다.
즉, 자바에서는 배열을 복사하는 작업이 굉장히 느리다는 게 원인인 것 같다.
반면 C언어는 굉장히 빠르기 때문에 C언어로 테스트했을 때는 퀵 정렬과 합병 정렬의 속도가 크게 차이 나지 않았지만
자바로 테스트했을 때는 속도 차이가 많이 나게 된 것 같다.
(코딩 테스트는 C언어나 파이썬으로 하라는 이유가 이렇게 와닿네...)
어디까지나 제 추측일 뿐입니다. 다른 의견이 있다면 말씀해주세요! 🙏 (제발..!)
💡 느낀 점
- Java를 사용한다는 가정하에... 합병 정렬은 생각보다 정말 별로인 것 같다.
- clone 메서드가 더 느리다는 사실은 정말 충격적이다. 왜!!?! 왜!!
- 배열 복사에 필요한 시간이 시간 복잡도에 영향을 꽤나 미치는 것 같은데 이런 경우는 O(nlogn)이라고 표기하기에 좀 그렇지 않나...
📘 참고한 자료
'오늘은 뭘 배울까? > 알고리즘' 카테고리의 다른 글
| 중위 표기법과 후위 표기법 (13) | 2021.08.08 |
|---|---|
| 힙(Heap) 이란? (2) | 2021.06.25 |
| 퀵 정렬이란? (2) | 2021.05.27 |
| 셸 정렬이란? (0) | 2021.05.15 |
| 삽입 정렬이란? (0) | 2021.05.13 |




댓글