
1. 퀵 정렬
1-1. 퀵 정렬이란?
1-2. 예시
1-3. 소스코드
1-4. 퀵 정렬의 시간 복잡도
1-5. 퀵 정렬은 얼마나 빠를까?
1. 퀵 정렬
1-1. 퀵 정렬이란?
이름값 하는 정렬 방법이다. 평균적으로 꽤나 빠른 속도를 보여준다.
여기서 평균적으로라고 한 이유는 [목차 1-4]에서 설명할 예정이다.
아무튼 이렇게 빠르게 정렬할 수 있는 이유는 분할 정복 방법을 사용했기 때문이다.
분할 정복 방법이란 큰 문제를 작은 문제로 쪼개어 문제를 해결하는 방식이다.
한 번에 먹기에 너무 큰 음식이 있으면 잘라먹듯이
한 번에 들기에 너무 무거운 짐이 있으면 나눠 들듯이
큰 문제를 해결하기 쉬운 작은 문제로 쪼개자는 것이다.
퀵 정렬은 이 개념을 도입한 방법인데 어떻게 정렬되는 건지 다음 목차에서 알아보자.
1-2. 예시

위와 같은 배열을 정렬한다고 해보자.
- 첫 번째 바퀴

가장 먼저 해야 할 것은 기준값으로 사용할 pivot(피벗)을 정하는 것이다.
여러 방법이 있지만 여기서는 가운데에 위치한 값을 사용할 것이다.
pivot은 구분하기 쉽게 그림에서 한 칸 띄워놓았다.
그다음에는
좌 -> 우로 탐색하며 pivot보다 큰 값을 찾고
우 -> 좌로 탐색하며 pivot보다 작은 값을 찾는다.

| 탐색을 계속 해야하는 조건 | 실제 값 비교 | 탐색을 해야하는가? |
| left < pivot | 3 < 5 | O |
| right > pivot | 2 < 5 | X |
이므로 right는 그대로 두고 left는 다음 인덱스로 이동한다.

| 탐색을 계속 해야하는 조건 | 실제 값 비교 | 탐색을 해야하는가? |
| left < pivot | 7 > 5 | X |
| right > pivot | 2 < 5 | X |
이제 조건에 부합하는 left와 right를 찾았으니 두 값을 swap 해준다. ( 7 <-> 2 )

| 탐색을 계속 해야하는 조건 | 실제 값 비교 | 탐색을 해야하는가? |
| left < pivot | 4 < 5 | O |
| right > pivot | 8 > 5 | O |
둘 다 조건에 맞지 않는다. 다음 인덱스로 넘어가자.

| 탐색을 계속 해야하는 조건 | 실제 값 비교 | 탐색을 해야하는가? |
| left < pivot | 5 = 5 | X |
| right > pivot | 1 < 5 | X |
둘 다 조건에 맞으므로 swap을 해준다.

left와 right를 이동하다가 이렇게 엇갈리게 되는 경우 탐색을 중지한다.

이렇게 pivot보다 작은 그룹과 큰 그룹으로 분할이 되었다.
이때 mid(pivot)은 작은 그룹에 속해있어도 되고 큰 그룹에 속해있어도 된다.
작은 그룹에 속하면 나중에 정렬이 완료되었을 때 가장 오른쪽에 위치할 거고
큰 그룹에 속하면 가장 왼쪽에 위치할 것이다.
나중에 잘게 쪼개진 그룹을 합친다고 생각해본다면 어느 그룹에 속해도 상관없다는 말을 이해할 수 있을 것이다.
- 두 번째 바퀴

이제 나누어진 그룹으로 각각 다시 분할을 반복하면 된다.
그룹에 속해있는 원소가 1개일 때까지 반복하면 퀵 정렬이 끝난다.
1-3. 소스코드
public class Test {
public static void main(String[] args) throws IOException {
int[] arr = { 3, 1, 7, 4, 5, 1, 8, 2 };
quickSort(arr);
for (int a : arr) {
System.out.println(a);
}
}
public static void quickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
private static void quickSort(int[] arr, int left, int right) {
// 더 이상 분할이 되지 않으면 종료
if (left >= right) return;
int mid = partition(arr, left, right);
quickSort(arr, left, mid - 1);
quickSort(arr, mid, right);
}
// 분할
private static int partition(int[] arr, int left, int right) {
int pivot = arr[(left + right) / 2];
// 엇갈리지 않으면 계속 반복
while (left <= right) { // 1. 배열에 값이 중복해서 들어가는 경우는 <=
// left와 right 찾기
while (arr[left] < pivot) left++;
while (arr[right] > pivot) right--;
// 엇갈리지 않으면 swap
if (left <= right) { // 2. 1과 동일
swap(arr, left, right);
left++;
right--;
}
}
return left;
}
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}코드는 재귀 함수로 작성하면 쉽게 작성할 수 있다.
# 주석 1.
만약 배열에 값이 중복해서 들어가는 경우 '<='를 해주어야 무한루프에 빠지지 않는다.
중복이 없다면 '<'만 해주어도 상관없다.
# 주석 2.
주석 1과 동일하다.
1-4. 퀵 정렬의 시간 복잡도
앞서 [목차 1-1]에서 퀵 정렬이 빠른 이유는 분할 정복 방법을 사용했기 때문이라고 했었다.
예를 들어, 버블 정렬로 숫자 10개를 정렬한다고 해보자.
이때 시간 복잡도는 O(n²), 즉 10 * 10 = 100이 된다.
이번에는 10개의 숫자를 5개 + 5개로 분할해서 정렬한다고 해보자.
이때 시간 복잡도는 5 * 5 = 25이니 25 + 25 = 50이 된다.
분할을 함으로써 시간 복잡도가 줄어드는 것이다. -> 퀵 정렬이 빠른 이유이다.
앞에서 든 예시처럼 분할했을 때 그룹의 개수가 딱 이쁘게 반으로 딱딱 떨어진다고 했을 때
퀵 정렬의 시간 복잡도는 O(n*logn)이 된다.
하지만 그룹의 개수가 비대칭으로 특히 한쪽으로 쏠려서 1개 / 9개 이런 식으로 나눠지는 경우
퀵 정렬의 시간 복잡도는 O(n²)가 된다.
즉, 일반적인 경우에 퀵 정렬은 굉장히 빠르지만 숫자들이 거의 정렬되어 있거나 역순인 경우 효율이 좋지 않다는 단점이 있다.
그렇기 때문에 pivot을 정하는 일은 시간 복잡도에 큰 영향을 끼친다.
어떤 값을 pivot으로 설정하느냐에 따라 시간 복잡도가 달라지기 때문이다.
pivot을 설정하는 방법은 여러 가지가 있다.
- 0번째 인덱스
- 가운데 인덱스
- 랜덤으로 설정
개인적으로 두 번째 방법이 가장 낫다고 생각이 든다.
대학교에서 첫 번째 방법으로 배웠던 기억이 있어서 코드를 짜려고 시도해 봤는데 이 경우 단점이 있었다.

9, 7, 8, 2, 4, 1이라는 숫자가 있을 때
'9'를 pivot으로 설정하고 left를 찾아가는 과정을 상상해보자.
이렇게 제일 큰 값이 0번째 인덱스에 있는 경우는 left를 찾지 못하고 모든 인덱스를 검사해야 할 뿐만 아니라
outBoundIndex 에러까지 매번 검사를 해주어야 한다. (배열 범위 초과)
인터넷에 올라와있는 꽤 많은 코드들이 이러한 상황을 고려하지 않은 듯하였다.
가운데 인덱스를 pivot으로 잡는 경우
left가 인덱스를 증가해나가다가 pivot에서 멈추기 때문에
배열 범위를 초과할 일도, 매번 범위 검사를 해야 할 필요도 없기 때문에 이 방법이 제일 낫다고 생각한다.
1-5. 퀵 정렬은 얼마나 빠를까?
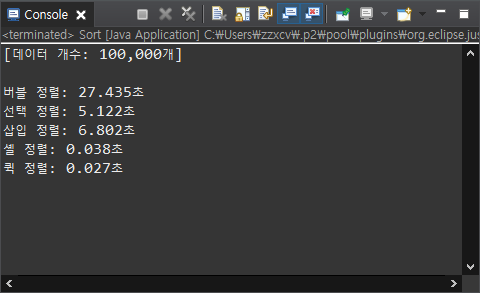
말로만 들어서는 얼마나 빠른지 감이 안 오기 때문에
데이터 100,000개를 정렬하는 데 얼마나 시간이 걸리는지 측정해보았다.
빠르긴 빠르네..
💡 느낀 점
- 대학교 다닐 때 퀵 정렬 헷갈려서 싫었는데... 포스팅 하다 보니 익숙해져 버림
- 정렬들의 속도를 정리해놓은 표를 보면 퀵 정렬보다 빠른 정렬도 있는데 왜 감히(?) 이놈이 퀵이라는 이름을 차지하게 된 걸까? 나머지 정렬을 마저 다 공부하면 알 수 있겠지..?
- 셸 정렬과 퀵 정렬을 합치면 단점을 커버한 정렬을 만들 수 있지 않을까라는 궁금증이 생겼음
📘 참고한 자료
'오늘은 뭘 배울까? > 알고리즘' 카테고리의 다른 글
| 힙(Heap) 이란? (2) | 2021.06.25 |
|---|---|
| 합병 정렬(=병합 정렬) 이란? (0) | 2021.05.30 |
| 셸 정렬이란? (0) | 2021.05.15 |
| 삽입 정렬이란? (0) | 2021.05.13 |
| 선택 정렬이란? (0) | 2021.05.12 |




댓글