
1. 삽입 정렬
1-1. 삽입 정렬이란?
1-2. 예시
1-3. 소스코드
1-4. 삽입 정렬의 시간 복잡도
1. 삽입 정렬
1-1. 삽입 정렬이란?
정렬 방법 중 가장 느린 버블 정렬
버블 정렬보다 조금 빠른 선택 정렬
그리고 선택 정렬보다 조금 빠른 것이 오늘 배울 삽입 정렬이다.
이미 정렬되어있는 수열 중 자신이 들어가야 할 위치를 찾아 삽입한다 하여 삽입 정렬이라는 이름이 붙었다.
말로만 들어서는 이해가 잘 안 가니 다음 예시를 통해 알아보자.
1-2. 예시
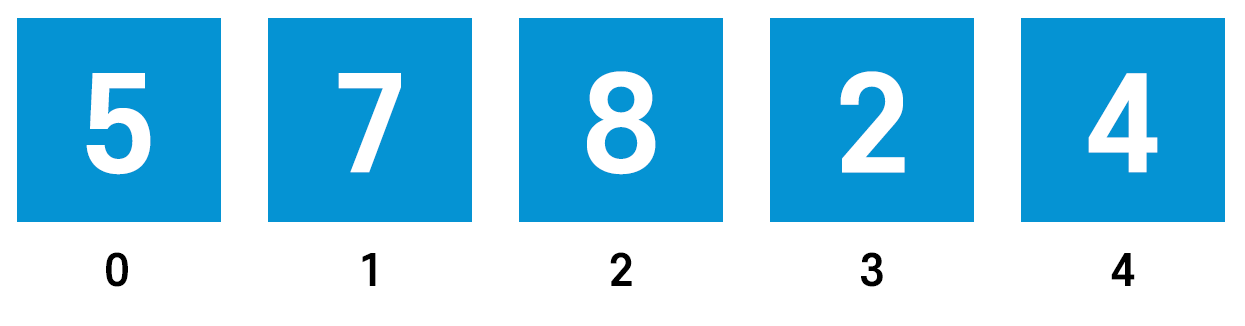
위와 같은 숫자를 정렬한다고 치자.
- 첫 번째 바퀴

[5]와 [7]을 비교해보자.
자리 바꿈이 필요할까? NO!
그렇다면 다음으로 넘어가자.
- 두 번째 바퀴

[7]와 [8]을 비교해보자.
자리 바꿈이 필요할까? NO!
그렇다면 다음으로 넘어가자.
- 세 번째 바퀴

[8]과 [2]를 비교해보자.
자리 바꿈이 필요할까? YES!
순서가 5, 7, 2, 8이 되었다.
[7]과 [2]를 비교해보자.
자리 바꿈이 필요할까? YES!
순서가 5, 2, 7, 8이 되었다.
[5]과 [2]를 비교해보자.
자리 바꿈이 필요할까? YES!
순서가 2, 5, 7, 8이 되었다.
- 네 번째 바퀴

세 번째 바퀴에서 그리했듯, [4]도 이전 인덱스의 값과 비교하면서 제 자리를 찾아가면 된다.

정렬이 완료되었다!
1-3. 소스코드
public static void insertionSort(int[] arr) {
for(int i=1; i<arr.length; i++) {
int temp = arr[i];
int j = i-1;
// 삽일할 위치를 찾으면서 이전 값들을 땡겨옴
while(j > 0 && arr[j] > temp) {
arr[j+1] = arr[j];
j--;
}
// 삽입할 위치를 찾았으니 삽입!
arr[j+1] = temp;
}
}[목차 1-2]에서 쉬운 이해를 위해 삽입할 위치를 찾아가는 과정에서 반복적으로 swap을 했지만
삽입 위치를 찾는 반복문을 시작하기 전에 값을 미리 temp에 담아두면 swap을 한 번만 실행해도 된다.
예를 들어 2, 3, 1을 삽입 정렬한다고 했을 때 [목차 1-2]에서의 설명한 방법은 아래와 같다.
2, 3, 1 · · · · · 3 > 1 이므로 swap
2, 1, 3 · · · · · 2 > 1 이므로 swap
1, 2, 3 · · · · · 정렬 완료
하지만 이번 [목차 1-3]에서 설명하고자 하는 방법은 아래와 같다. 우선 temp에 1을 넣어두고 시작한다.
2, 3, 1 · · · · · 3 > temp(1) 이므로 3 대입
2, 3, 3 · · · · · 2 > temp(1) 이므로 2 대입
2, 2, 3 · · · · · 삽입할 위치를 찾았으니 temp 대입
1, 2, 3 · · · · · 정렬 완료

swap이 줄어듬으로써 얼마나 시간이 줄어드는지 실제로 테스트해보았다.
.
.
.
.
.
.
.
.

어.. 어쨌든 조금이라도 빠르면 좋은 게 좋은 거니까!!
그리고 코드도 더 간결해진다. 그러니까 [목차 1-3] 방법을 사용하자!
1-4. 삽입 정렬의 시간 복잡도
삽입 정렬은 최악의 경우에 n-1, n-2, ... 1번을 반복하게 되며 이걸 식으로 바꾸면 n(n-1)/2번이다.
즉 O(n²)의 시간 복잡도를 가진다.
하지만 다음과 같은 상황에서는 어떨까?

이미 정렬이 되어있는 수열이 주어지면 자리 바꿈이 일어나지 않고
딱 한 번씩 앞의 숫자와 비교 검사를 하기 때문에 이러한 Best 상황에서는 O(n)의 시간 복잡도를 가진다.
즉, 만약 위 예시처럼 거의 정렬이 되어있는 수열이 주어진다면
버블 정렬, 선택 정렬, 삽입 정렬 중에서는 삽입 정렬이 가장 유리하다.
하지만 역순에 가까운 수열이 주어지거나, 숫자들의 개수가 너무 많다면 그만큼 비교와 자리 바꿈 횟수가 많아지므로
삽입 정렬을 사용하기에 부적합하다.
💡 느낀 점
- 거의 정렬되어 있는 수열이 주어졌을 때 삽입 정렬보다도 유리한 정렬이 있을까? 앞으로 정렬 시리즈를 계속 포스팅하면서 시간 측정 비교를 계속해봐야겠다.
- 맨날 선택 정렬과 삽입 정렬이 뭔가 비슷해서 헷갈렸는데 이제 절대 안 헷갈릴 것 같다.
📘 참고한 자료




댓글