
1. 버블 정렬
1-1. 버블 정렬이란?
1-2. 움짤로 보는 예시
1-3. 글로 보는 예시
1-4. 소스코드
1-5. 버블 정렬의 시간 복잡도
1. 버블 정렬
1-1. 버블 정렬이란?
버블 정렬이란 거품이 뽀글뽀글 올라가는 것처럼 보인다고 해서 붙여진 이름이다. (네이밍 너무 귀엽잖아.. 🥰)
이름도 귀엽고 정렬 중에는 구현하기 가장 쉬운 편에 속해서 개인적으로 제일 좋아했던 정렬이었으나
알고리즘 공부를 하면서 이놈이 효율이 쓰레기 좋지 않다는 것을 알게 되고 전혀 쓰지 않는다.
심지어 내장 기능으로 탑재된 정렬이 이것보다는 좋아서.. 버블 정렬은 "이걸 써먹겠어!"라고 해서 배우기보다는
정렬이란 무엇인가... 어떤 것들이 있는가... 를 알아보기 위해 배우는 것이다.
기본적인 개념은 말로 백번 설명하는 것보다 눈으로 한 번 보는 게 이해가 잘 가니 다음 목차로 넘어가자.
1-2. 움짤로 보는 예시

이 움짤은 다른 블로그에서 주워왔는데 원 출처는 알고리즘 도감이라는 앱인 것 같다. (앱이 꽤 괜찮다. 추천!)
움짤을 보면 맨 오른쪽에서부터 왼쪽으로 한 칸씩 이동하며 숫자 2개를 비교한다.
만약 오른쪽 숫자가 작으면 두 숫자의 자리를 바꾸고
오른쪽 숫자가 더 크면 자리를 바꾸지 않는다.
그렇게 한 바퀴를 돌고 나면 '1'이 맨 왼쪽에 위치하게 되며 '1'은 더 이상 정렬을 할 필요가 없어진다.
(회색으로 색이 바뀌는 이유가 정렬이 끝났다는 의미이다)
그렇게 처음에는 8번을 돌며 숫자를 비교하고...
그다음에는 7번..
그다음에는 6번..
.
.
.
마지막에 1번 비교하는 것 까지 하면 정렬이 완료되는 것이 바로 버블 정렬이다.
1-3. 글로 보는 예시

움짤이 너무 빨라서 이해가 잘 안 된다면 글로도 예시를 알아보자.
움짤에서는 왼쪽으로 이동해가며 비교를 했지만 그 반대로도 할 수 있다.
이번 목차에서는 오른쪽으로 이동해가며 비교하는 예시이다.
숫자는 위 사진과 같이 5, 7, 8, 2, 4가 주어졌다.
- 첫 번째 바퀴

앞에서부터 숫자를 2개씩 비교한다.
왼쪽 숫자(5)가 오른쪽 숫자(7) 보다 작다.
그러면 자리 바꿈을 하지 않고 넘어간다.

인덱스를 하나 늘려 또 2개의 숫자를 비교해보자.
왼쪽 숫자(7)가 오른쪽 숫자(8) 보다 작다.
그러면 자리 바꿈을 하지 않고 넘어간다.

이번엔 왼쪽 숫자(8)가 오른쪽 숫자(2) 보다 크다.
그러면 자리 바꿈을 한다.

바로 이렇게! 짠!

그다음 왼쪽 숫자(8)와 오른쪽 숫자(4)를 비교해서 자리 바꿈을 해준 모습이다.
(이제부터 과정 설명 생략)
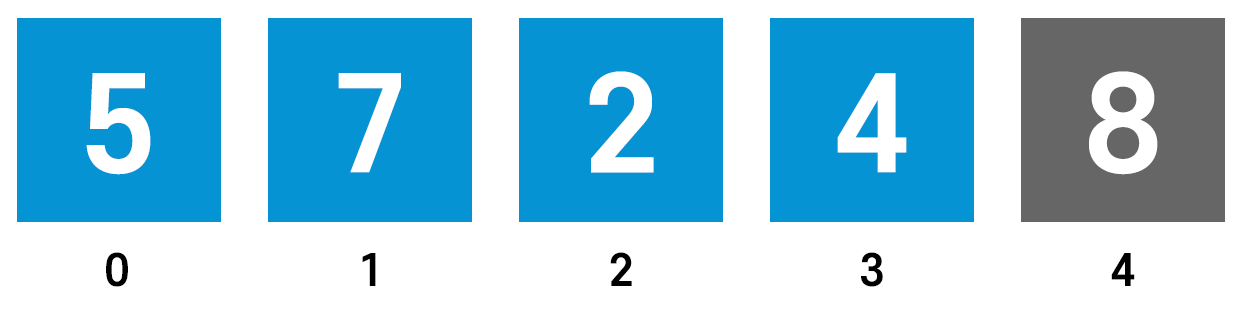
이렇게 하면 8이 제 자리를 찾아갔고 더 이상 4번째 인덱스는 비교 검사를 해주지 않아도 된다.
이렇게 버블 정렬은 한 바퀴를 돌 때마다 검사해야 할 인덱스가 하나씩 줄어든다.
두 번째 바퀴부터는 계속 비교 검사 & 자리바꿈의 연속이므로 자세한 설명은 생략 ㅎㅎ..
- 두 번째 바퀴




- 세 번째 바퀴



- 네 번째 바퀴


1-4. 소스 코드
public static void bubbleSort(int[] arr) {
for(int i=0; i<arr.length-1; i++) {
for(int j=1; j<arr.length-i; j++) {
if(arr[j-1] > arr[j]) {
int temp = arr[j-1];
arr[j-1]= arr[j];
arr[j] = temp;
}
}
}
}
1-5. 버블 정렬의 시간 복잡도
[목차 1-2]에서 설명했듯이 버블 정렬은 n-1, n-2, ... 1번을 반복하게 되며 이걸 식으로 바꾸면 n(n-1)/2번이다.
즉 O(n²)의 시간 복잡도를 가진다.
버블 정렬은 다른 정렬에 비해 자리 바꿈이 빈번히 일어나기 때문에 효율이 굉장히 낮다고 할 수 있다.

만약 주어진 수열이 이미 오름차순으로 정렬되어 있는 경우라도 기존의 방법으로는 무조건 반복문을 4번 돌아야 하지만 "교환이 한 번도 일어나지 않는다면 이미 정렬이 된 것으로 간주하고 반복문을 탈출한다"는 조건을 넣는다면
Best Case에서 O(n²)가 아닌 O(n)의 시간 복잡도를 갖는다.
💡 느낀 점
- 암만 생각해도 버블 정렬은... 꼭 버블 정렬을 써야 하는 상황은... 없는 것 같다.
📘 참고한 자료




댓글